Significado de Transversal: O que é, Conceito, Definição
Uma reta é chamada de transversal se corta ou cruza pelo menos duas outras retas. Os ângulos que uma transversal faz com as linhas cruzadas em torno dos pontos de interseção são chamados de ângulos transversais. Para cada linha cruzada, existem quatro ângulos transversais. Pares específicos desses ângulos tornam-se iguais se as linhas cruzadas forem paralelas.
Indice
- O que é uma transversal?
- Linhas transversais
- Ângulos transversais
- Ângulos formados por retas paralelas e transversais
- Ângulos formados por retas não paralelas e transversais
- Ângulos internos e externos alternativos
- Propriedades da Transversal
- Teorema Transversal
- Como exatamente alguém pode reconhecer uma transversal?
- Qual é a representação gráfica do transversal?
- Como você rotula uma transversal?
- Exemplos de Transversal
- Exemplo 1
- Solução
- Exemplo 2
- Solução
- Conclusão
- Outros significados
- Postagens relacionadas:
O que é uma transversal?
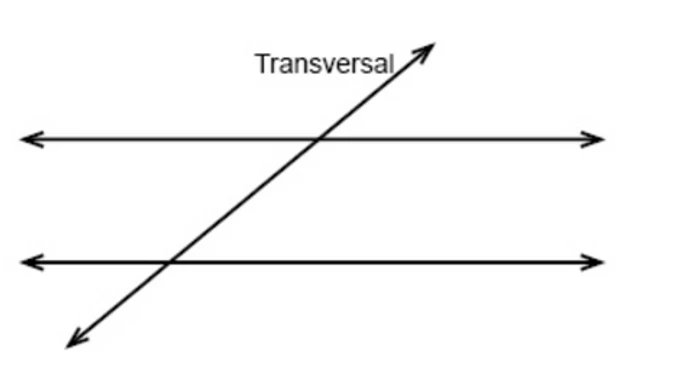
No campo da geometria, uma linha transversal é uma linha que passa por duas outras linhas dentro do mesmo plano em dois pontos diferentes. No plano euclidiano, as transversais são um componente essencial no processo de produção de paralelismo entre duas ou mais retas adicionais. Ele encontra duas linhas em pontos diferentes onde elas se sobrepõem. A interseção que resulta da Transversal cria vários ângulos. Esses são chamados de ângulos correspondentes, ângulos co-interiores, ângulos alternativos internos e ângulos alternativos externos.
Linhas transversais
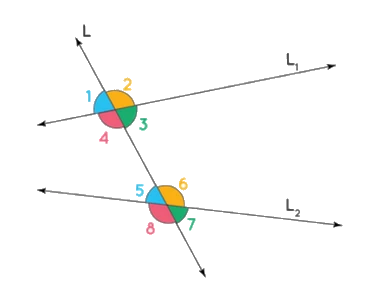
No campo da matemática, uma transversal é qualquer linha que, em locais distintos, cruza duas outras linhas retas. No diagrama a seguir, a linha denominada “ L ” é uma linha transversal que cruza as linhas denominadas “ L1 ” e “ L2 ” em dois locais separados. Dentro do reino das retas paralelas e das retas transversais, uma reta transversal é o que une duas retas paralelas.
Ângulos transversais
Uma transversal cria vários ângulos diferentes, incluindo lados e ângulos, ângulos externos de inclinação, pares de pontos de interseção, pares de ângulos alternos internos, pares de ângulos alternos externos e pares de ângulos internos que estão do mesmo lado da transversal. . Cada um desses ângulos pode ser subdividido em subtipos adicionais. Cada um desses ângulos pode ser determinado em qualquer cenário, que pode se referir a linhas paralelas ou não paralelas.
Ângulos formados por retas paralelas e transversais
Quando linhas ou cortes transversais sobre duas linhas paralelas, os ângulos criados como resultado tem a mesma medida. Portanto, os ângulos produzidos pela primeira linha que intercepta a transversal produzem ângulos equivalentes aos ângulos correspondentes produzidos pela segunda linha que intercepta a transversal.
Ângulos formados por retas não paralelas e transversais
Se uma transversal intercepta duas linhas que não são paralelas, os ângulos resultantes não têm conexão entre si, embora ambos sejam os resultados do mesmo evento. Elas não são idênticas umas às outras, como é o caso das linhas paralelas, mas todas se correspondem. Da mesma forma, não há conexão entre os ângulos interior e exterior, lateralmente opostos e sucessivos quando uma transversal corta a interseção de duas linhas que não são paralelas entre si.
Ângulos internos e externos alternativos
Os ângulos produzidos quando uma transversal cruza duas retas coplanares são ângulos alternos internos. Eles estão exatamente do mesmo lado das linhas paralelas que as linhas paralelas. No entanto, eles estão em lados opostos da Transversal.
A Transversal corta através de duas linhas coplanares em dois lugares diferentes, então continua até o terceiro ponto. Os valores desses ângulos indicam se as duas retas aqui apresentadas são paralelas ou não. Se esses ângulos forem iguais entre si, então as linhas que a transversal cortam serão paralelas.
Ângulos externos alternos são os pares de ângulos produzidos no lado externo das retas paralelas e no lado oposto da Transversal. Esses ângulos só podem ser gerados quando as linhas paralelas e transversais são desenhadas em direções opostas.
Propriedades da Transversal
As seguintes características podem ser especificadas sempre que a interseção de duas retas paralelas produz uma transversal.
A medida de cada ângulo formado por um par de ângulos semelhantes é a mesma para cada Transversal que corta duas retas paralelas.
Quando uma transversal corta 2 linhas paralelas, os ângulos internos de cada par de linhas alternadas são os mesmos.
Cada combinação de ângulos internos situados no mesmo lado de uma transversal é considerada suplementar se uma transversal intercepta duas retas paralelas.
Teorema Transversal
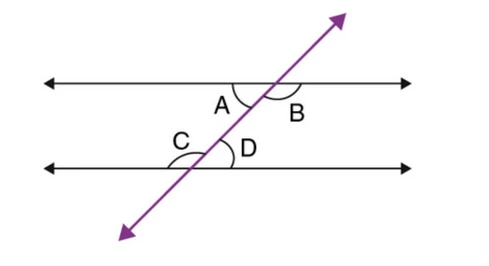
Vários teoremas, incluindo o seguinte, foram definidos para Transversal:
Se uma transversal corta duas linhas paralelas, então o ângulo formado por cada par correspondente dessas linhas é o mesmo.
Duas retas são consideradas paralelas se uma transversal as corta de tal forma que um par de ângulos formados pela interseção são proporcionais entre si.
Duas retas são consideradas paralelas se uma transversal as corta de modo que um par de ângulos alternos internos sejam proporcionais entre si.
Diz-se que uma transversal tem ângulos internos suplementares para qualquer par de ângulos internos que estão exatamente do mesmo lado da transversal quando ela encontra duas linhas paralelas.
Como exatamente alguém pode reconhecer uma transversal?
Por cruzar duas ou mais linhas em pontos diferentes, o Transversal é fácil de detectar e identificar.
Qual é a representação gráfica do transversal?
Em matemática, não existe um símbolo específico que possa ser usado para representar uma transversal.
Como você rotula uma transversal?
Uma transversal pode ser rotulada da mesma forma que outras linhas em geometria, o que significa que podemos usar o alfabeto. Por exemplo, a linha PQ representa a Transversal das linhas AB e CD.
Exemplos de Transversal
Exemplo 1
Três arqueiros atiraram flechas que atingiram uma árvore. A seta X e a seta Y são paralelas ao solo, e a seta Z atravessa as outras duas setas. Se as flechas X e Y fazem um ângulo maior de 140°, então em que ângulo o terceiro arqueiro lançou a flecha Z?
Solução
Vamos considerar que o ângulo que a flecha Z está fazendo é A então,
140° + A = 180°
A = 180° – 140°
A = 40°
Exemplo 2
Considere uma transversal que intercepta duas retas paralelas, A e B. O ponto onde ela intercepta a linha A está em um ângulo de 75°, e o ponto onde ela intercepta o ponto B é desconhecido. Determine o ângulo de interseção da transversal com o ponto B.
Solução
Encontrar o ângulo usando a propriedade de linhas paralelas cortadas por uma transversal. Usando a propriedade do ângulo interior alternativo para encontrar o ângulo desconhecido.
B + 75° = 180°
B = 180° – 75°
B = 105°
Conclusão
O texto explica o significado de transversal como aquilo que cruza, que atravessa ou que se apresenta de modo oblíquo em relação a um referente. O texto também apresenta alguns exemplos do uso de uma transversal em diferentes circunstâncas na geometria.
Outros significados
Postagens relacionadas:
- Significado da Tatuagem de Medusa: Uma Janela para o Poder e Mistério - março 15, 2024
- Obá: a divindade das águas doces nas tradições afro-brasileiras - dezembro 6, 2023
- Significado de Amizade Reciproca, Platônica, Colorida, Virtual - setembro 8, 2023
Recomendado Para Você




